Glossário
Aqui apresentamos alguns conceitos necessários para a compreensão e apresentação de Gramáticas no contexto de Linguagens Formais. Usaremos como exemplo os (a) alfabetos latinos (a, b, c… z) e (b) binários (0 e 1)
-
Alfabeto ou Vocabulário
Conjunto finito não vazio de símbolos, onde os símbolos os elementos do alfabeto.
(a) {a, b, c, …, z}
(b) {0, 1}
-
Cadeia ou Palavra
Concatenação de símbolos de um alfabeto.
(a) abc, aaa, leonardo, antonio, raul…
(b) 0, 1, 10, 11, 100…
-
Cadeia Nula (símbolo especial λ)
Símbolo para representar uma cadeia de comprimento zero, λ
-
Comprimento de Cadeia
Número total de símbolos em uma cadeia
(a) |antonio| = 7; |leo| = 3; |raul| = 4
(b) |0| = 1; |10| = 2; |100| = 3
-
Concatenação de Cadeias (operação +)
Concatenação dos símbolos de duas ou mais cadeias. Seja a concatenação z = x + y
(a) x = abc; y = xyz; z = abcxyz
(b) x = 01; y = 10; z = 0110
-
Produto de Alfabetos (operação X ou .)
Producto cartesiano de alfabetos
(a)X(b) = {a0, a1, b0, b1, …, z0, z1}
-
Exponenciação de Alfabetos (operação A^N)
Alfabetos compostos de cadeias de comprimento N sobre o alfabeto original. (produto cartesiano de um alfabeto com ele mesmo).
(a) a^1 = a; a^2 = {aa, ab, ac, …, az, ba, bc,bb, …, bz, …}; a^3 = {aaa, aab, aac, …}
(b) b^1 = b; b^2 = {00, 01, 10, 11}; b^3 = {000, 001, 010, …}
-
Fecho (operação *)
Conjunto de todas as cadeias de qualquer comprimento sobre um determinado alfabeto. União de todas as exponenciações deste alfabeto
(a) {abc, aaa, leonardo, antonio, raul, aaa, bbbbb, kdsadksasadsa, sadasd, dfgdfg…}
(b) {0, 1, 10, 11, 100, 1111, 01010101, 111, 010101, 1010101, 10000…}
-
Linguagem
Coleção de cadeias de símbolos sobre um alfabeto/vocabulário. Estas cadeias são denominadas sentenças da linguagem, e são formadas pela justaposição de elementos individuais, os símbolos da linguagem.

Gramáticas, introdução
As gramáticas foram criadas para tentar definir em um modelo linguagens comuns como inglês, português, etc. Falhando neste objetivo, as definições formais criadas serviram, e muito bem, as necessidades de definição de Linguagens de Programação (LPs).
Uma gramática formal define o processo através do qual podem ser geradas todas as sentenças (conjunto de cadeias) de determinada linguagem. Note como, no exemplo abaixo (de uma sentença da língua inglesa), a construção da sentença ‘just do it’ se inicia no não terminal sentença, e se deriva em outros não terminais, como adjetivo, verbo e outros.

Usando este exemplo, vamos nomear algumas coisas em nossa gramática (da língua inglesa).
-
Não Terminais (ou variáveis)
Símbolos que permitem que a gramática defina suas leis de formação (ex.: sentença, adjetivo, verbo…)
-
Terminais
Símbolos que constituem as sentenças da linguagem (ex.: todas as palavras em inglês)
-
Produções
Relações entre os Terminais e Não Terminais (ex.: adverbio -> ‘just’)
-
Símbolo Inicial
Não Terminal que gera todas as cadeias da sentença (ex.: sentença)
Gramáticas, definição
Formalmente as gramáticas são definidas por quádruplas (conjuntos de quatro coisas) ordenadas:
G = (Vn, Vt, P e S)

-
Vn - vocabulário não terminal
Este vocabulário corresponde ao conjunto de todos os símbolos dos quais a gramática se vale para definir as leis de formação das sentenças da linguagem.
-
Vt - vocabulário terminal
Símbolos que constituem as sentenças da linguagem. Dá-se o nome de terminais aos elementos de Vt.
-
P - leis de formação
Conjunto de todas as leis de formação utilizadas pela gramática para definir a linguagem.
-
S - símbolo inicial
Principal categoria gramatica de G; é dito o símbolo inicial ou o axioma da gramática. Indica onde se inicia o processo de geração de sentenças.
Para melhor ilustrar, abaixo seguem duas gramáticas exemplo, que demonstram os elementos da quádrupla gramatical:
G1 = ({S, B}, {a, b, c}, P, S) G2 = ({S}, {a, b}, P, S)
P = { P = {
1. S -> aBSc 1. S -> aSbb
2. S -> abc 2. S -> abb
3. Ba -> aB }
4. Bb -> bb
}
Processo de Derivação
O processo de derivação de uma gramática permite a identificação das cadeias que pertencem à linguagem definida por esta gramática, como um processo de leitura, verificação, validação de uma sentença. Neste contexto, derivar é o processo de ‘sair’ do símbolo inicial para uma cadeia composta apenas de terminais. Para efetivar a derivação, utilizamos as leis de formação (terceiro elemento da quadrupla, P) e, para melhor ilustrar o processo, vamos derivar as menores cadeias contidas em G1.
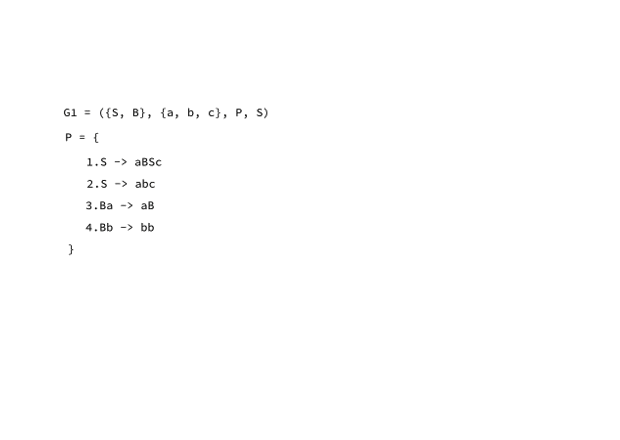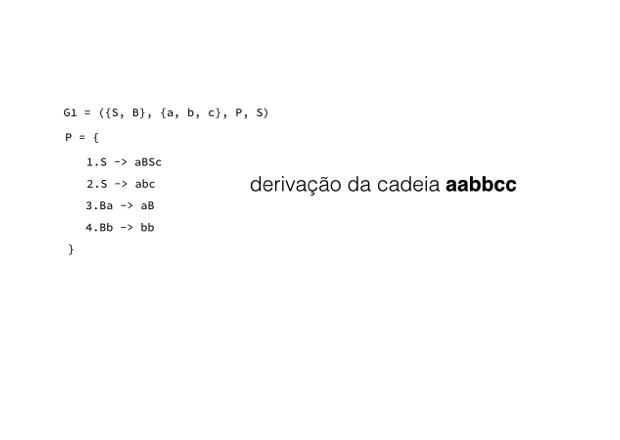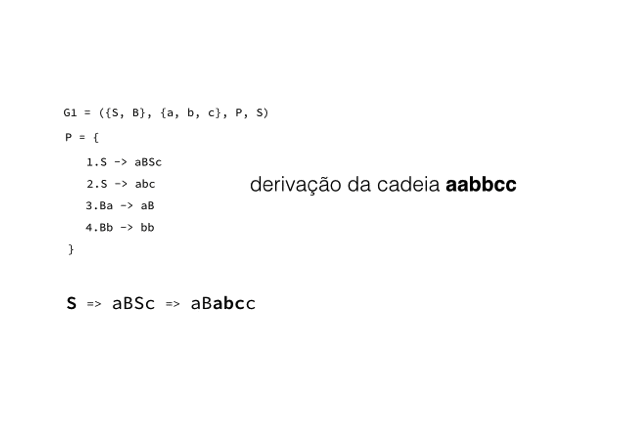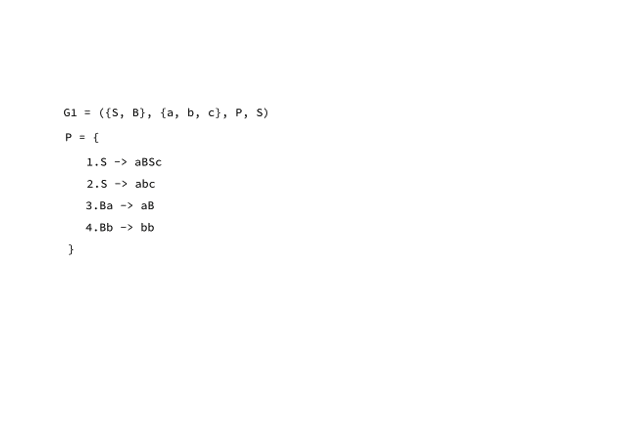
Hierarquia de Chomsky
A definição de gramáticas e as linguagens geradas por elas é bastante ampla e nos permite descrever uma enorme gama de possíveis linguagens. O problema dessa irrestribilidade na concepção de gramáticas está no estudo e desenvolvimento de compiladores. O reconhecimento de uma gramática muito generalizada é complicado e, além disso, muitas vezes desnecessária para a aplicação em linguagens de programação de interesse.
Para controlar a generalidade das gramáticas foram criadas uma série de restrições e, mais importante que isso, uma hierarquia de gramáticas definidas pelas restrições impostas a elas. Essa hierarquia é chamada de Hierarquia de Chomsky.
-
Tipo 3: Gramáticas Regulares (GR)
Neste tipo, a forma das gramáticas é restrita a dois formatos possíveis
A -> aB ou A -> a
(linear unitária à direita)
OU
A -> Ba ou A -> a
(linear unitária à esquerda)
-
Tipo 2: Gramáticas Livres de Contexto (GLC)
A restrição imposta é que, em uma regra de substituição, o ‘lado esquerdo’ deve apenas conter um símbolo não terminal (ex.: AB -> aa não é permitida). As linguagens geradas são chamadas linguagens livres de contexto.
-
Tipo 1: Gramáticas Sensíveis ao Contexto (GSC)
É imposta uma restrição às regras de substituição, nenhuma substituição pode reduzir o comprimento da sentença onde é aplicada. (ex.: uma regra Saa -> Sa não é permitida). As linguagens geradas são chamadas linguagens sensíveis ao contexto.
-
Tipo 0: Gramáticas Irrestritas (GI)
Não possuem restrição alguma, as linguagens geradas por essas gramáticas são chamadas linguagens de estrutura de frase.
Para ver exercícios práticos sobre Hierarquia de Chomsky clique aqui.


